Jacinda's Game of Weed
When the PM refused to disclose her vote on the referendum for legalizing cannabis, many lauded her for sticking to her principles for not wanting to unduly influence the public. But, was this the game she was actually playing? Let's have a look…

(originally published on LinkedIn on October 31, 2020)
This starts off badly: I got into a Twitter argument about Prime Minister Ardern’s decision not to disclose her vote in the cannabis referendum so as not to use her popularity in influencing the public decision.
Let’s use a game-theoretic analysis to see if the PM’s choice of strategy makes sense.
The Game of Influence
In Figure 1: PM’s game we write the logic of the stated decision. If PM announces her vote (whatever it is) then due to her huge popularity it will swing some votes, and not swing others. PM wanted to leave the decision to the NZ public. Because she did not know how many (if any) decisions would be swayed (proportion X in the game tree), she did not want to disclose her vote. If she did not disclose, this had no effect of swinging voters. She moved first.

Figure 1: PM’s game
Now, a quick note about games from the game-theoretic point of view. Every move by every player is an action. It is clear from the above game tree and the PM’s announcement, that choosing not to announce is a conscious and communicated choice.
Another thing that should be clear, is that communicated choices by hugely popular people have an influencing effect on others. That’s a black-and-white statement, with which people are free to disagree. In that case, the same people who disagree should also accept that any statement by anyone has no influence on anyone, and therefore no politician’s utterances are of any value. If this were true, then the PM’s alternatively communicated choice of her actual position would have had no impact—and we would have had the actual game as in Figure 2: PM’s game of no influence.
I think we can all agree that the updated game is unlikely to represent the reality—but at least it is internally consistent. In this game, there is no difference in announcing or not announcing.
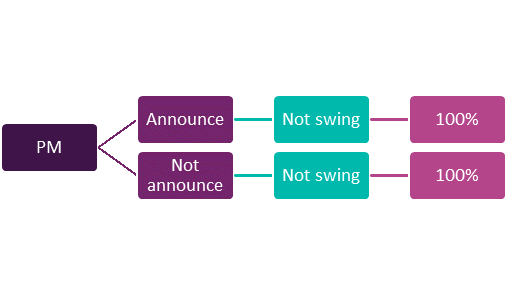
Figure 2: PM’s game of no influence
Now, let’s go with the belief that announcements do, in fact, matter. This is defensible—if it were not so, we would have had neither marketing nor politics; both exist and we in fact know the behavioural-theoretic underpinnings of the value of signals, influencing, and coordination. In this case, the updated PM’s game is as in Figure 3: PM’s game of influence, where (and this is critical!) her every action has an influencing possibility.

Figure 3: PM’s game of influence
In Figure 3: PM’s game of influence, it is clear that the action of no announcement is itself a signal with influencing power. This, on its own, will have influenced a certain proportion of the population (Y). If Y < X then the logic of “I don’t announce because I don’t want to provide undue influence” might make sense, but only with a qualification “I know I will influence some either way, and I believe that I will influence fewer people by not announcing”. This is not a position that was communicated or defended.
However, in this particular scenario, we just don’t know the relative proportions of X & Y. The whole point of the exercise is to show that you can’t have your cake and eat it, too.
Corollary: The vocal non-action by a popular personality is in itself a strong signal that has influencing power. Get used to it. Unless you know for sure X & Y, keeping mum is not a defensible strategy, if the goal is to not influence.
The Game of Uncertainty
Now, let’s dig deeper. The game in Figure 1 is not the correct representation of reality (it equates to having your cake and eating it, too) but games in Figure 2 and Figure 3 are in fact sub-games, depending on the beliefs about the world, as both sets are internally consistent. Thus, the proper (full) game is in fact in Figure 4: PM’s game with uncertainty.
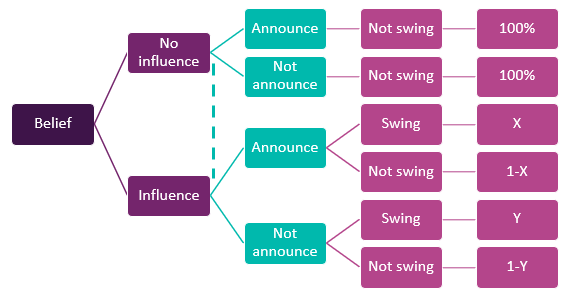
Figure 4: PM’s game with uncertainty
Note, I highlight PM’s point of view and PM’s payoffs only. Because PM doesn’t know which world she’s in (influence or no influence) she cannot be sure about the non-existence of “swing” move by the public; this uncertainty is represented by the dotted line indicating not knowing where one’s at (from PM’s point of view). The public of course knows whether they are influenced or not, so theirs is basically the sub-game represented as in Figure 2.
Regardless of the beliefs, what is clear is that “I do not announce because I don’t want to create an undue influence” is not a defensible strategy, exactly because either the non-announcement itself is an influencing move or no move is an influencing move. Again, can’t have your cake and eat it, too.
Other Opinions on the Internet: Are They Relevant to the Evaluation of the Chosen Strategy?
But let’s examine some other opinions floating around the internet:
- Binding vs non-binding—this is irrelevant for evaluating the internal consistency of the choice of strategy. The game stays the same with the knowledge that this is, in fact, a non-binding referendum.
- This is a referendum and not part of a campaign—true, and given that this policy isn’t Labour-initiated, it’s correct for Prime Minister Ardern not to campaign on this. However, this is a different game to which we’ll turn shortly.
- This is the pinnacle of the democratic process because the public educates itself and decides freely—this is flawed from several angles (as support for the actual choice):
- First, a vocal non-action exercises its own “undue influence” as we’ve just seen, defeating the goal of “no influence”;
- Second, any politician on a campaign trail tries to influence public—this is, in fact, part and parcel of the democratic process, so saying this action would've been undemocratic seems strange;
- Third, by this logic we should leave all decisions to referenda and not allow any politician ever to utter anything, lest they unduly influence the public, clearly a nonsensical position;
- Fourth, the statements of politicians are themselves a critical part of the public education, especially on the complex issues of public import that include elements of health policy, social justice, and other critical matters of public interest—therefore, withholding an opinion is sub-optimal if the goal is to have educated public decision-making (unless, again, there is a different game afoot, to which we turn next). And if people disagree with this, then the same people should also hold that politicians add no value whatsoever when educating the general public on issues of public interest, and therefore should keep mum on any and all issues (see the third point above).
Instead of thinking about “undue influence” it feels more helpful to think about the public interest—especially because there was a lot of misinformation and personal opinions on this particular topic. We can expand the game to include the choices of other politicians, including Judith Collins, providing their own & strongly influencing, opinions—was it in the public’s best interest to have this particular influence left unanswered, not counterbalanced by that of the PM? Who made a value judgement of which influence was “due” and which “undue”?
The Game of Politics
So, to recoup, if the PM was playing the “I don’t want to unduly influence public” game, then the stance of the “no announcement” strategy is not defensible, as either every PM action would have had an influence (she is, after all, a hugely popular person, and for good reasons) or it would’ve been irrelevant.
But was she? I.e. was this the game she was actually playing, in a game-theoretic sense?
Because the actions are not consistent with the stated desire, as we’ve seen, there are two ways of looking at it:
- PM logic of influencing was flawed;
- PM played a different game.
I find the first to be unsatisfactory, because by all accounts Prime Minister Ardern is an incredibly intelligent woman, and she has a group of strong advisors around her.
Which brings me to the point that she was playing a different game, namely the one of politics, not “undue” influence. Let me rephrase: the influence she wanted to exhibit was not on the Yes/No for cannabis—it was to get the centre-right voters to support the Labour party.
Consider Figure 5: PM’s game of politics. If she announced, who would change their vote? Given the support base of the Left, it stands to reason the only people who would’ve changed their vote are centre-right swing voters. Where would they go? The other (non-influenced and therefore non-alienated) voters would either go to the Labour or the Greens. So, the critical proportion is the X that would’ve been alienated and had gone to National. (I’m simplifying and ignoring the Act for now, because I believe a libertarian party to be favourable to personal freedom of choice.)
If the PM doesn’t announce, who would be alienated? The core Labour or Green-leaning supporters with a strong feeling towards “Yes” vote. Where would they go? To the Greens; call this the proportion Y. The other votes would be unchanged.
In reality, the relative size of Y vs X doesn’t even matter, because losing Y to the Greens is still a much more favourable outcome for the Labour than losing X to the National party, regardless of the size of Y (within any realistic range). For the realistic beliefs about the sizes of X and Y, this game has a dominant strategy: not to announce.
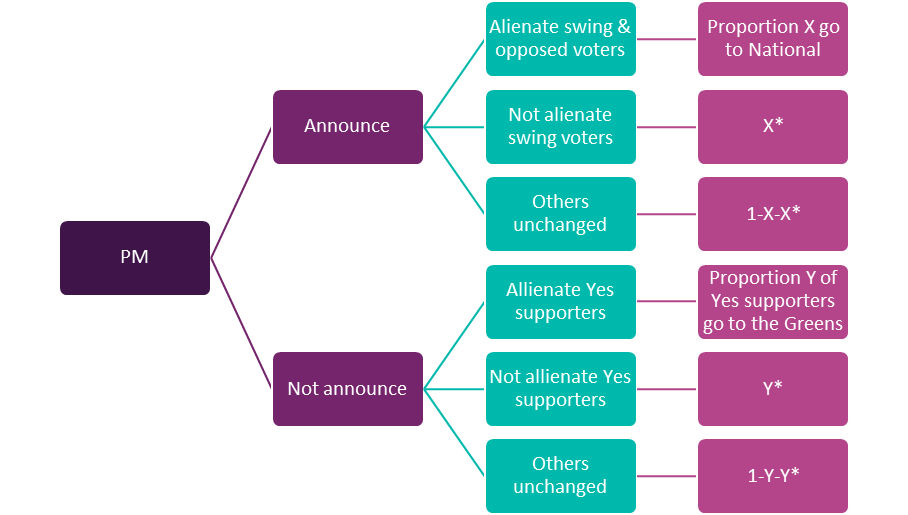
Figure 5: PM’s game of politics
Does this look like the real game that the PM was playing? I’d say yes: the moves make much more sense, i.e. they are internally consistent, there is no logical incongruity between the motivation and the chosen strategy. It makes rational, political sense.
Conclusion: Know the Game You’re Playing
In conclusion, I’m fine with the game PM was really playing. It feels like one of politics, and that’s great—after all, her job was to get Labour in as best a position to form the next Government as possible. Mission accomplished and done so masterfully and with flair.
I have two final messages.
To all: if you’re considering strategies, know the game you’re playing, and know the game others are playing. If these aren’t the same game, think carefully.
My message to the unabashed fans on the internet who use lazy logic and flawed arguments to defend whatever the move, regardless of the merits of the move. Let’s celebrate this as a shrewd political move (because it was) and not a morally high ground stance on the issue: the former is much more consistent with the reality, while the latter is found wanting.
P.S.
If you're new to game theory or (like me) it's been a while since you derived the maths for Selten's trembling-hand perfect equilibrium, I highly recommend Barry Nalebuff's & Avinash Dixit's The Art of Strategy: A Game Theorist's Guide to Success in Business and Life. It's really-really good; I'll be using some examples from here when teaching an Exec Ed course on decision-making under uncertainty (watch this space + inquiries welcome).





